Эратосфен биография и вклад в географию, математику и другие науки

Таблица простых чисел

Простые числа, для удобства их дальнейшего использования, записывают в таблицу, которую называют таблицей простых чисел. Ниже представлена таблица простых чисел до 1 000.

Возникает логичный вопрос: «Почему мы заполнили таблицу простых чисел только до 1 000, разве нельзя составить таблицу всех существующих простых чисел»?

Ответим сначала на первую часть этого вопроса. Для большинства задач, при решении которых придется использовать простые числа, нам будет вполне достаточно простых чисел в пределах тысячи. В остальных случаях, скорее всего, придется прибегать к каким-либо специальным приемам решения. Хотя, несомненно, мы можем составить таблицу простых чисел до сколь угодно большого конечного целого положительного числа, будь то 10 000 или 1 000 000 000, в следующем пункте мы поговорим о методах составления таблиц простых чисел, в частности, разберем способ, получивший название .

Теперь разберемся с возможностью (а точнее с невозможностью) составления таблицы всех существующих простых чисел. Мы не можем составить таблицу всех простых чисел, потому что простых чисел бесконечно много. Последнее утверждение представляет собой теорему, которую мы докажем после следующей вспомогательной теоремы.

Теорема.

Наименьший положительный и отличный от 1 делитель натурального числа, большего единицы, является простым числом.

Доказательство.

Пусть a – натуральное число, большее единицы, и b – наименьший положительный и отличный от единицы делитель числа a. Докажем, что b – простое число методом от противного.

Предположим, что b – составное число. Тогда существует делитель числа b (обозначим его b₁), который отличен как от 1, так и от b. Если также учесть, что абсолютная величина делителя не превосходит абсолютной величины делимого (это мы знаем из свойств делимости), то должно выполняться условие 1<b₁<b.

Так как число a делится на b по условию, и мы сказали, что b делится на b₁, то понятие делимости позволяет говорить о существовании таких целых чисел q и q₁, что a=b·q и b=b₁·q₁, откуда a= b₁·(q₁·q). Из правил умножения целых чисел следует, что произведение двух целых чисел есть целое число, тогда равенство a=b₁·(q₁·q) указывает на то, что b₁ является делителем числа a. Учитывая полученные выше неравенства 1<b₁<b, мы получаем противоречие условию, что b – наименьший положительный и отличный от единицы делитель числа a.

Теперь мы можем доказать, что простых чисел бесконечно много.

Теорема.

Простых чисел бесконечно много.

Доказательство.

Предположим, что это не так. То есть, предположим, что простых чисел всего n штук, и эти простые числа есть p₁, p₂, …, p_n. Покажем, что мы всегда можем найти простое число, отличное от указанных.

Рассмотрим число, p равное p₁·p₂·…·p_n+1. Понятно, что это число отлично от каждого из простых чисел p₁, p₂, …, p_n. Если число p — простое, то теорема доказана. Если же это число составное, то в силу предыдущей теоремы существует простой делитель этого числа (обозначим его p_n+1). Покажем, что этот делитель не совпадает ни с одним из чисел p₁, p₂, …, p_n.

Если бы это было не так, то по свойствам делимости произведение p₁·p₂·…·p_n делилось бы на p_n+1. Но на p_n+1 делится и число p, равное сумме p₁·p₂·…·p_n+1. Отсюда следует, что на p_n+1 должно делиться второе слагаемое этой суммы, которое равно единице, а это невозможно.

Так доказано, что всегда может быть найдено новое простое число, не заключающееся среди любого количества наперед заданных простых чисел. Следовательно, простых чисел бесконечно много.

Итак, в силу того, что простых чисел бесконечно много, при составлении таблиц простых чисел всегда ограничивают себя сверху каким-либо числом, обычно, 100, 1 000, 10 000 и т.д.

биография

Первые годы

Особенности развития географической науки в современном мире

Эратосфен родился примерно в 276 г. до н.э. в Кирене, греческом городе, расположенном в Северной Африке, на территории, которая сейчас является территорией Ливии

Он был сыном Аглауса, о котором не ведется никаких исторических записей, поэтому считается, что он не был из важной семьи в то время

Несмотря на то, что Эратосфен не имел выдающегося происхождения, он приехал из города, который получил признание людей, которые родились в нем. Кирена была основана греками Теры до 600 г. до н.э. и процветала как независимый город до прихода эллинской эры..

Кирена была поглощена Птолемейской монархией Египта, которая управляла Александрией, культурным и торговым центром Средиземноморья. Был большой книжный магазин, музей и школа повышения квалификации.

Эратосфен пошел по стопам других ученых в своем городе и обучался у Лисании, эксперта по грамматике. Несмотря на то, что в греческие времена молодые люди из богатых семей имели больший доступ к образованию, для мужчин существовали академии.

Дети с семи лет обучались таким предметам, как литература, спорт и музыка. Считается, что Эратосфен также мог быть учеником Каллимах.

Афины

Основным интересом Эратосфена к юности была философия, и это призвание привело его в Афины в возрасте 15 лет. Там он оставался примерно 25 лет. Затем он подготовил и приобрел известность как академический.

В Афинах он нашел так много философов, что он был поражен и поражен. Сначала он учился у Зенона в школе стоиков. Также с одним из его учеников, Аристоном де Хиосом, из которого он написал биографию. Но он не нашел в них стиля, который ему нравился.

Затем он присоединился к платоникам как ученик Арцесилао. Именно тогда Эратосфен создал произведение под названием Platonicus, в которой, следуя методу Платона, он исследовал математические и космологические темы. В то время он также написал Пери Агатōн кай какōN, текст, который был потерян.

После этих переживаний он разочаровался в философии и решил посвятить себя поэзии. Так началась слава Эратосфена, так как в своей новой области он добился признания, которого хотел.

Тексты не сохранились от его первых произведений в качестве поэта; однако некоторые имена передавались потомкам в цитатах других греков. Гермес это была одна из его работ, в которой он обратился к жизни бога, а другой взял по имени Эригона.

Александрия

Считается, что именно слава Эратосфена как поэта привлекла внимание Эвергетеса Птолемея III, который призвал его в Александрию, чтобы он занялся репетиторством своего сына, а также предложил ему должность директора городской библиотеки.. Птолемей III был тронут не только интересом к работе Эратосфена, но и политическими соображениями

Город Кирена прошел независимый период Египта до брака между Птоломео III и Беренис, дочерью Магаса, губернатора этого города

Птолемей III был тронут не только интересом к работе Эратосфена, но и политическими соображениями. Город Кирена прошел независимый период Египта до брака между Птоломео III и Беренис, дочерью Магаса, губернатора этого города.

В поисках защиты своего недавно восстановленного домена Птолемей III видел, как хорошо удовлетворить жителей Кирены, предлагая Эратосфену такую же должность, как глава великой Александрийской библиотеки..

В период, когда Эратосфен руководил Александрийской библиотекой, в ней были достигнуты большие успехи. Приобретенные произведения, такие как великие драмы Эсхила и Еврипида. Они также расширили исследования в Софокла.

В эту эпоху Эратосфен воспользовался своим положением и доступом к информации, которую ему пришлось изучать по самым разным предметам. Однако он никогда не хотел специализироваться на одном предмете, поэтому некоторые упрекали его.

смерть

Эратосфен умер в Александрии, около 194 г. до н.э., когда ему было 82 года. Некоторое время назад он ослеп в результате катаракты и, как полагают, совершил самоубийство от голода.

Несмотря на его большой вклад в науку, его работа не была воспроизведена многими другими, по-видимому, потому что у него не было достаточно студентов, чтобы передать свои открытия и теории.

Тем не менее, его вклад в изучение земли дал ему титул отца географии. В течение своей жизни Эратосфен был любителем знаний во всех областях.

Реализация

Биография президента азербайджана ильхама алиева

Сразу приведём реализацию алгоритма:

int n;
vector<char> prime (n+1, true);
prime = prime1 = false;
for (int i=2; i<=n; ++i)
	if (primei)
		if (i * 1ll * i <= n)
			for (int j=i*i; j<=n; j+=i)
				primej = false;

Этот код сначала помечает все числа, кроме нуля и единицы, как простые, а затем начинает процесс отсеивания составных чисел. Для этого мы перебираем в цикле все числа от до , и, если текущее число простое, то помечаем все числа, кратные ему, как составные.

При этом мы начинаем идти от , поскольку все меньшие числа, кратные , обязательно имеют простой делитель меньше , а значит, все они уже были отсеяны раньше. (Но поскольку легко может переполнить тип , в коде перед вторым вложенным циклом делается дополнительная проверка с использованием типа .)

При такой реализации алгоритм потребляет памяти (что очевидно) и выполняет действий (это доказывается в следующем разделе).

Удивительная история

Баранский николай николаевич: биография, карьера, личная жизнь

Древнегреческий мыслитель изучал историю, философию, литературу и множество других дисциплин. Современники посмеивались над ним и считали дилетантом, поскольку, по их мнению, он интересовался всем, но толком не знал ничего. Однако ученого это не смущало. Эратосфен работал в египетской Александрии. Однажды, возвращаясь из своего музея, он повстречал путешественников, идущих из Сиены — города, расположенного южнее Александрии, на Северном тропике (современное название — Асуан). Те поделились с ученым любопытным наблюдением: когда они находились в Сиене (а это был самый длинный день в году), ни один предмет в городе не отбрасывал тень.

Эратосфен не мог оставить сказанное без внимания, поэтому спустя год посетил Сиену и убедился, что путники его не обманули. Он заглянул в глубочайший городской колодец и увидел: солнечные лучи достигают его дна, а также подметил, что светило в данный момент располагалось ровно над головой. В это же время в Александрии оно висело гораздо ниже и абсолютно все предметы, на которые падали лучи, отбрасывали небольшую тень. Такое простое наблюдение натолкнуло Эратосфена на мысль об определении размеров Земли.

Эратосфен и география

Ученый был первым, кто дал географии ее имя, которое означает, что география изучает не только обитаемые области, но всю Землю.

В работе «География», состоящей из 3-х книг, ученый представил научный обзор всех греческих достижений, обосновал «математическую» географию, высказал взгляд на Землю, как шарообразное тело, привел данные о поверхности. Ученый попытался оценить расстояния до Солнца и Луны и их размеры. В работе описаны затмения Солнца и Луны, высказано предположение о длительности дня на разной широте.
Его главное открытие – размер земного шара, вычисленный геометрически. Для этого он предпринял путешествие из Александрии в Сиену (современный Асуан).

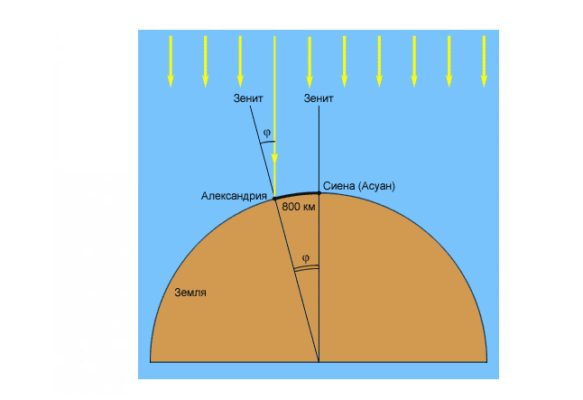Рис. 1. Измерение и расчет Эратосфеном радиуса Земли.

Длина экватора, вычисленная Эратосфеном отличается от полученной современными методами всего на 385 км; это было самое точное определение того времени.

Не менее важное определение – угол наклона земной оси, сделанное не менее точно.
Предложена идея плавания к Индии, которая подтолкнула путешественника Колумба к разработке маршрута через Атлантику. Приложением к «Географии» была карта мира, созданная ученым

На карте впервые появились параллели и меридианы.

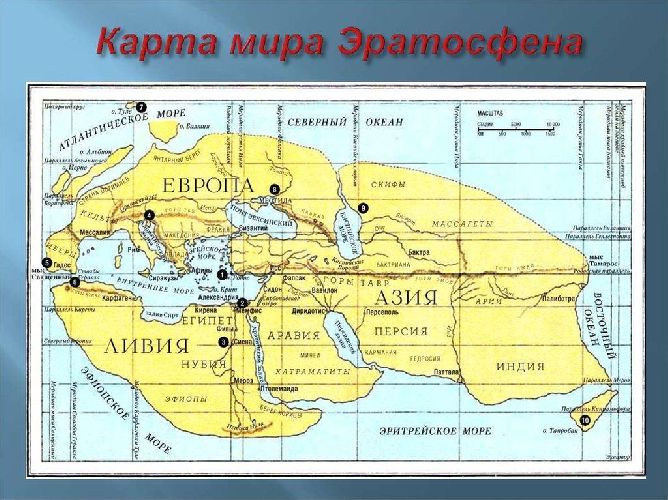Рис. 2. Карта Эратосфена.

Литература[править | править код]

Античная география. М., 1953.
Бобынин В. В. Эратосфен // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Дитмар А.Б. Родосская параллель: Жизнь и деятельность Эратосфена. — М.: Мысль, 1965. — 72 с.
Колчинский И.Г., Корсунь А.А., Родригес М.Г. Астрономы: Биографический справочник. — 2-е изд., перераб. и доп. — Киев: Наукова думка, 1986. — 512 с.

На иностранных языках

Aujac G. Eratosthène de Cyrène, le pionier de la geographie. — Paris: Édition du CTHS, 2001. — 224p.
Diller A. Geographical Latitudes in Eratosthenes, Hipparchus and Posidonius // Klio. — 1934. — Bd. 27. — Heft 3. — S. 258—269.
Dutka J. Eratosthenes’ measurement of the Earth reconsidered. Archive for History of Exact Sciences, 46, 1993, p. 55-64.
Fraser P. M. Ptolemaic Alexandria. — Oxford: Clarendon Press, 1972.
Goldstein B. R. Eratosthenes on the measurement of the Earth // Historia Mathematica. — Vol. 11. — 1984. — P. 411—416.
Rawlins D. Eratosthenes’ geodesy unraveled: was there a high-accuracy Hellenistic astronomy, Isis, 73, 1982, p. 259—265.
Rawlins D. The Eratosthenes — Strabo Nile map. Is it the earliest surviving instance of spherical cartography? Did it supply the 5000 stades arc for Eratosthenes’ experiment?, Arch. Hist. Exact Sci, 26 (3), 1982, p. 211—219.
Rawlins D. Eratothenes’s large earth and tiny universe. DIO, 14, 2008.
Shcheglov D. A. Ptolemy’s System of Seven Climata and Eratosthenes’ Geography // Geographia Antiqua. — Vol. 13. — 2004 (2006). — P. 21-37.
Thalamas A. La géographe d’Ératosthène. — Versailles, 1921.
Wolfer E. P. Eratosthenes von Kyrene als Mathematiker und Philosoph. — Groningen-Djakarta, 1954.

На страже знаний

Узнать о том, что открыл Эратосфен в географии, 7 классу будет интересно еще и потому, что этот ученый по праву считается одним из мужей, кто своими усилиями оформил целый ряд научных направлений и отраслей знаний, которые способствовали славе Александрийской библиотеки.

Например, именно при Эратосфене в библиотеке были созданы целые отделы, сотрудники которых занимались переписью и изучением великих греческих поэтов, таких как Эсхил, Софокл, Еврипид и, конечно, Гомер.

Столь широкий круг интересов и неудержимая энергия стали причиной присвоения Эратосфену нескольких почетных прозвищ, наиболее расхожими среди которых были «пятиборец», что указывало на его всестороннюю развитость, и «бета», которое свидетельствовало о глубочайшем почтении, которое современники испытывали к великому филологу, признавая за ним статус настолько высокий, что опережал его лишь Платон.

Асимптотика

Докажем, что асимптотика алгоритма равна .

Итак, для каждого простого будет выполняться внутренний цикл, который совершит действий. Следовательно, нам нужно оценить следующую величину:

Вспомним здесь два известных факта: что число простых, меньше либо равных , приблизительно равно , и что -ое простое число приблизительно равно (это следует из первого утверждения). Тогда сумму можно записать таким образом:

Здесь мы выделили первое простое из суммы, поскольку при согласно приближению получится , что приведёт к делению на нуль.

Теперь оценим такую сумму с помощью интеграла от той же функции по от до (мы можем производить такое приближение, поскольку, фактически, сумма относится к интегралу как его приближение по формуле прямоугольников):

Первообразная для подынтегральной функции есть . Выполняя подстановку и убирая члены меньшего порядка, получаем:

Теперь, возвращаясь к первоначальной сумме, получаем её приближённую оценку:

что и требовалось доказать.

Более строгое доказательство (и дающее более точную оценку с точностью до константных множителей) можно найти в книге Hardy и Wright «An Introduction to the Theory of Numbers» (стр. 349).

2. Работы и сочинения Эратосфена

2.1. Работы по математике

Из сочинений Эратосфена по математике до нашего времени дошло только написанное к царю Птолемею письмо об удвоении куба. Это письмо сохранилось в комментарии Евтокия к трактату Архимеда О шаре и цилиндре. В письме содержатся некоторые исторические сведения о делийской задаче, а также описание прибора, изобретённого самим автором и известного под именем мезолябия.

Сведения о других математических сочинениях Эратосфена отличаются крайней неполнотой. Папп в двух местах своего Собрания называет сочинение Эратосфена О средних величинах, замечая при этом, что оно во всех своих предположениях стоит в связи с линейными местами.

О сочинении Эратосфена Платоник, посвящённом пропорциям, говорит Теон Смирнский. Возможно, что именно к Эратосфену восходит алгоритм «разворачивания всех рациональных отношений из отношения равенства», описанный Теоном Смирнским и Никомахом Герасским.

Отрывок из ещё одного сочинения Эратосфена приводит во Введении в арифметику Никомах Герасский. То же делает и Ямвлих в своём комментарии к этому сочинению Никомаха. Предмет этого отрывка состоит в изложении найденного Эратосфеном способа определения произвольного количества последовательных простых чисел (так называемое решето Эратосфена).

2.2. Работы по астрономии

Из сочинений Эратосфена по астрономии до нашего времени дошло только одно, Катастеризмы — перечисление созвездий и заключающихся в них звёзд, числом до 700. Определения положений этих звезд сочинение не даёт.

Для своих астрономических наблюдений Эратосфен установил под портиком здания Мусейона большие армиллярные сферы.

Эратосфен определил угловое расстояние от экватора до тропика: он нашёл его равным 11/83 от 180°.

2.3. Работы по геодезии и географии

В тесной связи с астрономией находится работа Эратосфена, состоящая в измерении длины земного меридиана. Краткое изложение этой работы известно нам по трактату Клеомеда «О круговращении небесного свода»:

Измерение Земли по Эратосфену

Карта Эратосфена

Позднее полученное Эратосфеном число было увеличено до 252000 стадиев. Определить, насколько эти оценки близки к реальности, трудно, поскольку неизвестно, каким именно стадием пользовался Эратосфен. Но если предположить что речь идёт о греческом (178 метров), то его радиус земли равнялся 7,082 км, если египетским, то 6,287 км. Современные измерения дают для усреднённого радиуса Земли величину 6,371 км. Что делает выше описанный расчёт выдающимся достижением и первым достаточно точным расчётом размеров нашей планеты.

В сравнительно больших отрывках дошло до настоящего времени сочинение Эратосфена о географии. В полном своём составе оно делилось, по свидетельству Страбона, на три книги. В первой автор дал критический обзор истории географии, от первого появления географических понятий у Гомера до своих непосредственных предшественников, то есть до историков и географов, воспользовавшихся походами Александра Македонского и их описаниями. Вторая книга излагает основы географии по взглядам самого автора. Предмет третьей книги составляет суша.

2.4. Другие работы Эратосфена

Эратосфен является основателем научной хронологии. В своих Хронографиях он пытался установить даты, связанные с историей Эллады, составил список победителей Олимпийских игр.

Сохранились отрывки из сочинения Эратосфена О древней комедии и из двух его поэм; в одной он вкладывает в уста Гермеса рассказ о строении неба, светил и гармонии сфер, в другой передаётся легенда об Эригоне, дочери Икара.

Описание алгоритма

Наша цель — посчитать для каждого числа от в отрезке его минимальный простой делитель .

Кроме того, нам потребуется хранить список всех найденных простых чисел — назовём его массивом .

Изначально все величины заполним нулями, что означает, что мы пока предполагаем все числа простыми. В ходе работы алгоритма этот массив будет постепенно заполняться.

Будем теперь перебирать текущее число от до . У нас может быть два случая:

— это означает, что число — простое, т.к. для него так и не обнаружилось других делителей.

Следовательно, надо присвоить и добавить в конец списка .

— это означает, что текущее число — составное, и его минимальным простым делителем является .

В обоих случаях дальше начинается процесс расстановки значений в массиве : мы будем брать числа, кратные , и обновлять у них значение . Однако наша цель — научиться делать это таким образом, чтобы в итоге у каждого числа значение было бы установлено не более одного раза.

Утверждается, что для этого можно поступить таким образом. Рассмотрим числа вида:

где последовательность — это все простые, не превосходящие (как раз для этого нам понадобилось хранить список всех простых чисел).

У всех чисел такого вида проставим новое значение — очевидно, оно будет равно .

Почему такой алгоритм корректен, и почему он работает за линейное время — см. ниже, пока же приведём его реализацию.

Жизнь

Эратосфен, сын Аглаоса, родился в 276 г. до н.э. в Кирене . Теперь часть современной Ливии , Кирена была основана греками несколько веков назад и стала столицей Пентаполиса (Северная Африка) , страны , состоящей из пяти городов: Кирены, Арсинои , Береники , Птолемея и Аполлонии . Александр Великий завоевал Кирену в 332 г. до н.э., и после его смерти в 323 г. до н.э. ее правление перешло к одному из его полководцев, Птолемею I Сотеру , основателю Птолемеевского царства . При Птолемеях экономика процветала, в основном за счет экспорта лошадей и сильфия , растения, которое использовалось в качестве приправ и лекарств. Кирена стала местом культивирования, где расцветали знания. Как и любой молодой грек того времени, Эратосфен учился в местной гимназии , где он изучал бы физические навыки и социальный дискурс, а также чтение, письмо, арифметику, поэзию и музыку.

Эратосфен учение в Александрии по Бернардо Строцци (1635)

Эратосфен отправился в Афины для продолжения учебы. Там его основатель Зенон из Citium преподавал стоицизму философские лекции о добродетельной жизни. Затем он учился у Аристо Хиосского , который руководил более циничной философской школой. Он также учился под руководством главы Платонической академии , которым был Аркесилай Питанский . Его интерес к Платону привел к тому, что он написал свою первую научную работу « Платоникос» , исследуя математические основы философии Платона. Эратосфен был человеком многих взглядов и исследовал искусство поэзии при Каллимахе . Он писал стихи: одно в гекзаметрах под названием « Гермес» , иллюстрирующее историю жизни бога; и другой в элегии , названный Эригон , описывающий самоубийство афинской девушки Эригоны (дочери Икария) . Он написал « Хронографии» — текст, в котором с научной точки зрения указаны важные даты, начиная с Троянской войны . Эта работа была высоко оценена за точность. Позже Георгию Синчеллу удалось сохранить из хронографий список 38 царей египетских Фив . Эратосфен также написал « Олимпийские победители» , хронологию победителей Олимпийских игр . Неизвестно, когда он писал свои произведения, но они подчеркнули его способности.

Эти произведения и его великие поэтические способности привели фараона Птолемея III Эвергета к поиску места его библиотекарем в Александрийской библиотеке в 245 году до нашей эры. Эратосфен, которому тогда было тридцать, принял приглашение Птолемея и отправился в Александрию, где прожил всю оставшуюся жизнь. Примерно через пять лет он стал главным библиотекарем — должность, которую ранее занимал поэт Аполлоний Родий . В качестве главы библиотеки Эратосфен обучал детей Птолемея, в том числе Птолемея IV Филопатора, который стал четвертым фараоном Птолемея. Он расширил фонды библиотеки: в Александрии все книги нужно было сдавать для тиражирования. Было сказано, что они были скопированы настолько точно, что невозможно было сказать, вернула ли библиотека оригинал или копию. Он стремился поддержать репутацию Александрийской библиотеки, несмотря на конкуренцию со стороны Пергамской библиотеки . Эратосфен создал целый раздел, посвященный исследованию Гомера, и приобрел оригинальные произведения великих трагических драм Эсхила , Софокла и Еврипида .

Эратосфен внес несколько важных вкладов в математику и науку и был другом Архимеда . Около 255 г. до н.э. он изобрел армиллярную сферу . В О круговых движениях небесных тел , Клеомед приписывал ему рассчитав окружность Земли около 240 г. до н.э., с высокой точностью.

Эратосфен считал, что в каждой нации есть и хорошее, и плохое, и критиковал Аристотеля за то, что он утверждал, что человечество разделено на греков и варваров , а также за то, что он утверждал, что греки должны сохранять свою расовую чистоту. В возрасте около 195 г. до н.э. он заболел офтальмией и ослеп. Утрата способности читать и наблюдать за природой мучила его и подавляла, заставляя добровольно морить себя голодом. Он умер в 194 г. до н.э. в возрасте 82 лет в Александрии.

Заключение

Открытия Эратосфена внесли огромный вклад в науку и жизнь античного общества. После измерения окружности ученый произвел определение других параметров созданной им карты: расстояние между городами, торговыми путями, материками и островами. Он высчитал радиус планеты, оценил зависимость светового дня от ширины и долготы.

Изучив множество научных направлений, Эратосфен создал и ввел новое – географию. Сделанный им вклад стал решающим толчком в развитии картографии и астрономии. Тем не менее, эллин трудился в разных течениях и развивал Александрийскую библиотеку до потери зрения и смерти в 195 г. до н. э.